Capítulo 22

MODELACIÓN MATEMÁTICA DE PLANTAS DE TRATAMIENTO DE LODOS ACTIVADOS

Introducción

Uno de los modelos más conocidos y más utilizados para diseñar las plantas de tratamiento por lodos activados es el de MacCarty y Lawrence (1970). El modelo es una simplificación utilizada para diseñar las plantas, considerando un régimen estacionario y la DBO o DQO total como parámetro de caracterización. Este modelo es el eX_Puesto en los libros clásicos de tratamiento de aguas. No permite predecir el comportamiento dinámico de las plantas, ni determinar con exactitud la demanda de oxígeno y producción de lodos.

En los últimos años, aparecieron cambios importantes en las teorías y prácticas de diseño de los procesos biológicos de tratamiento de aguas residuales, constituyendo claramente un parteaguas (nuevo paradigma) entre el enfoque clásico, muchas veces empírico, y las tendencias actuales asentadas en la formulación de modelos mecanísticos más precisos. Estos modelos presentan todas las ventajas de la simulación dinámica, una mayor exactitud de las predicciones y diseño, y vuelven obsoleta una buena parte de las simplificaciones e imprecisiones de los métodos antiguos. Cambian, radicalmente, hasta los métodos de caracterizar las aguas residuales, con la aparición, por ejemplo, de una nueva forma de fragmentar la demanda química de oxígeno. Los modelos para los lodos activados (el más famoso de todos los procesos de tratamiento biológico, el cual se utiliza por ejemplo en las 2 macroplantas de Toluca, México) fueron desarrollados por un comité científico internacional bajo la responsabilidad de la prestigiosa IAWQ (Internacional Association of Water Quality), actual IWA. En el inicio, el esfuerzo de la comunidad científica radicó en llegar a un consenso sobre la forma de presentar los modelos y hacerlos evolucionar o ampliar progresivamente, según los conocimientos que se tienen en el curso de los años. Existen hoy cuatro generaciones de modelos de la IWA, el ASM1 original y el muy reciente ASM3, capaces de predecir la degradación de la materia orgánica, nitrificación y desnitrificación en lodos únicos, y el ASM2 y su versión modificada ASM2d que incluyen además la remoción biológica del fósforo.

En la actualidad, existen una grande necesidad de difusión del tema y actualización de los especialistas en modelación de los procesos de tratamiento de agua. También existen retos bien identificados para la investigación en los aspectos de caracterización y mecanismos bioquímicos así como en lo relacionado con la simplificación de los modelos y protocolos de simulación. El enfoque de la modelación dinámica en tratamiento de aguas está en vía de generalizarse a muchos otros tipos de sistemas (Ríos: Water Quality Model N°1, Reichert et al. 2001; Digestores: Anaerobic digestion Model N°1, Task group 2002), y constituye, sin duda alguna, uno de los polos con mayor potencial de desarrollo en el futuro para la investigación en tratamiento de aguas residuales.

Generalidades
Antecedentes históricos de la modelación dinámica del proceso de lodos activados

En 1982, la IAWQ incentivó la formación de un grupo de estudio internacional encargado de acelerar el desarrollo de la modelación dinámica de las plantas de tratamiento, crear una plataforma comuna consensual y proponer un modelo simple de inicio (“Task Group on Mathematical Modelling for Design and Operation of Activated Sludge Process”). El grupo concentró sus primeros esfuerzos en inventariar los modelos existentes así como los obstáculos a su desarrollo. Se llegó a concluir que los únicos modelos que conocieron una amplia difusión y nivel de utilización, fueron los más simples que consideran una hipótesis de régimen estacionario y mezcla completa para los reactores. Por otra parte, existía un gran número de modelos dinámicos, cuya difusión fue obstaculizada por la complejidad, la falta de orden para presentarlos y las limitaciones en el poder de las computadoras.

En los años 70, la Universidad de Cap Town (Sur_Africa) fue una de las pioneras de la modelación dinámica con los trabajos del profesor G.V.R. Marais. Otros trabajos tuvieron lugar después o simultáneamente en un número muy restringido de universidades de Europa y Estados Unidos. Parte de los pioneros fueron juntados luego en 1980 en el primer grupo de estudio de la IAWQ (actual IWA) formado por Henze (Dinamarca), Grady (USA), Gujer (Suiza) y Marais (Sur-Africa).

Las conclusiones del grupo fueron publicadas en 1987 (Task Group, 1987) en un informe que presentaba lo conocido hoy como el Modelo ASM1, modelo dedicado a describir la degradacion de materia orgánica, nitrificación y desnitrificación en un proceso de lodos activados (de tipo lodos únicos). Los logros más destacados del grupo fueron un consenso en los procesos biológicos que integran el modelo, la estandarización de los símbolos, la presentación del modelo utilizando una notación matricial, la propuesta de valores de “default” de los parámetros del modelo, la adopción de la DQO y su fraccionamiento para caracterizar las aguas y lodos, un código de programación para el desarrollo futuro de software de modelización. La última acción propulsó la existencia actual de varios softwares y programas que tienen implementados, los conceptos del ASM1 original o algunas de sus modificaciones para fines de diseño, operación de plantas o investigación: Aquasim, Biowin, GPS-X, SSSP, Simba, etc. Aquasim es un programa que se presta bien en la docencia e investigación (Reichert 1998).

En 1995, los trabajos del grupo de estudio renovado se prolongaron para publicar la versión ASM2, la cual está dirigida a predecir el comportamiento del fósforo. En 1999 hubo dos otras modificaciones con la aparición de la version ASM2d (versión modificada del ASM2) y de la versión ASM3 (alternativa al ASM1).

Ventajas y límites de la modelación dinámica

• La modelación dinámica permite predecir la calidad del efluente, la demanda de oxígeno y la producción de lodo en respuesta a las fluctuaciones en tiempo real de la carga y del caudal del influente.


• Una vez que se tiene modelado y calibrada una planta, el modelo se puede utilizar para fines de diagnóstico, proyección, comparación de variantes, probar cambios en la operación, evaluación de las prácticas actuales, optimización de operación y gastos, así como para la capacitación del personal.


• Aun cuando la planta proyectada no existe todavía físicamente, se puede probar configuraciones innovadas y comparar variantes.


• Se pueden reducir las necesidades de estudio piloto, el tiempo y la inversión que se requiere para esto, realizando primero los estudios por modelación y sólo probar en escala piloto algunas de las soluciones identificadas.


• Se puede optimizar la configuración y el funcionamiento de una planta de tratamiento, así como responder a numerosas preguntas respecto a su capacidad e impactos de modificaciones proyectadas.


• La modelación constituye un instrumento de ayuda a la decisión para los administradores de plantas y un medio de gráfico visual para convencer estos últimos.


• Con la modelación se pueden realizar estudios sin perturbar el funcionamiento de la planta, ni poner en riesgo sus equipos.
  
• Es también un medio de formación y conscientización de los operadores sobre algunos aspectos críticos.


• Como principales límites, se debe notar la necesidad de realizar estudios anteriores para calibrar los modelos. Los datos que se necesitan para esto son generalmente diferentes de los datos rutinarios de caracterización que se tienen en las plantas de tratamiento. Todavía falta realizar investigación para evaluar la aplicabilidad de los modelos para diferentes efluentes industriales.

Nociones básicas para la modelación
Constitución de los modelos

Los modelos son una descripción matemática de una serie de procesos que ocurren en un espacio delimitado (tanques y reactores). Sin embargo, uno debe darse cuenta que el hecho de que un modelo se ajuste bien a los datos eX_Perimentales y que prediga bien el comportamiento del sistema estudiado, no significa que los mecanismos del modelo son correctos del punto de vista microbiológico (Van Loosdrecht et al. 1999).

En tratamiento de aguas, los modelos se eX_Presan a través de balances de masas que toman en cuenta la cinética de reacción de los procesos (procesos de transformación), la hidrodinámica (tipo de flujo y mezcla en el reactor) y el transporte de materia a través de los límites del sistema (flujos de entrada y salida). Los procesos de transporte son unas características específicas a cada sistema: configuración del reactor, distribución del influente, mezcla, dispersión, recirculación, extracción de lodo, etc. Los procesos de transformación, por el contrario, ocasionan cambios en la estructura y nivel de los componentes químicos con una velocidad que depende del ambiente local del proceso. Los procesos individuales que forman el modelo son relacionados a través de ecuaciones de leyes de conservación de masas (balances), las cuales se deben resolver, para poder describir los cambios en el estado del sistema a través de las variables de estado (concentraciones de biomasa, oxígeno, DQO, nitrógeno, por ejemplo). La escritura de balances de masas de un modelo resulta en un sistema de ecuaciones diferenciales totales y o parciales y de ecuaciones algebraicas. Su resolución necesita en general algún programa o software. Algunos autores suelen presentar sus modelos exhibiendo sistemas de ecuaciones ya manipuladas, simplificadas o despejadas, lo que sólo dificulta su comprensión. Una forma sistemática de presentar los modelos y facilitar su entendimiento es a través de:

1. Una lista de componentes representados por variables de estado (formas de sustancias) involucrados en los procesos: matriz de concentraciones [C_i]


2. Una descripción de los procesos de transformación que afectan los componentes: modelos bioquímicos, coeficientes estequiométricos, eX_Presiones de ley de velocidad de reacciones.


3. Una caracterización del transporte convectivo de sustancias en los límites del sistema: diagrama de flujo.


4. Una caracterización de la dispersión y mezcla interna según el tipo de reactor/sistema, tanto para los componentes disueltos como para los sólidos suspendidos (sedimentación).

La notación matricial adoptada en el ASM1

Muchos modelos de lodos activados existen en la literatura y difieran entre ellos por la manera que se describen los procesos biológicos de transformación (modelos biocinéticos). Pero estos modelos venían presentados en forma de balances de masas, a veces con ecuaciones ya manipuladas o simplificadas, donde es difícil recobrar y aislar los diferentes procesos a la base del modelo. Esta forma de presentación fue uno de los obstáculos a la aceptación de los modelos por los practicantes (es muy frustrante buscar comprenderlos).

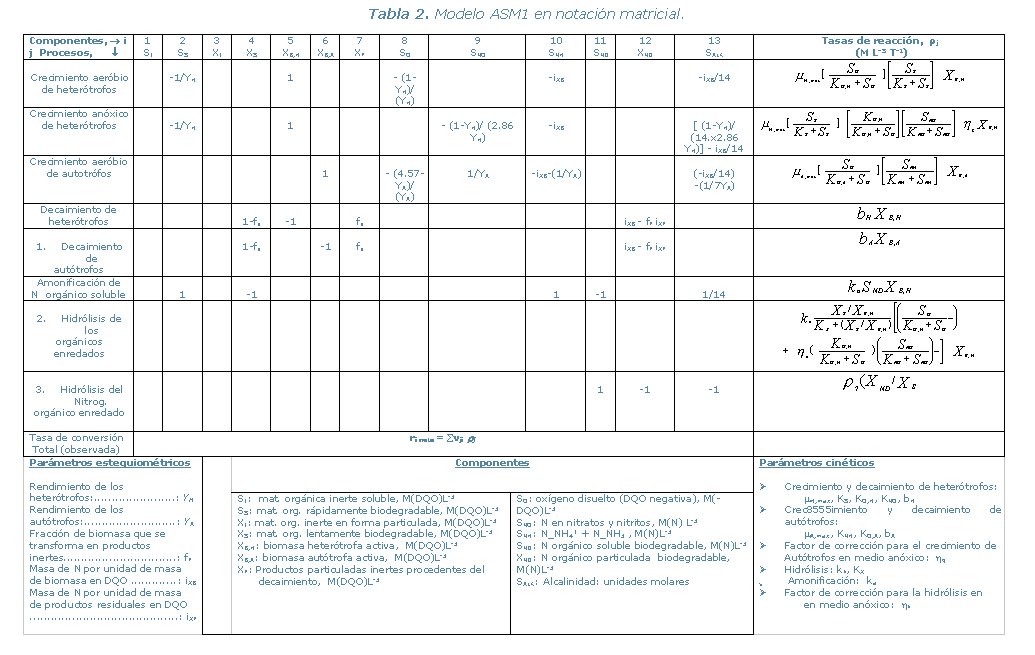
Una de las decisiones más importantes que tomó el “Task group” fue la de optar por una notación matricial. Este tipo de notación tiene su origen de Peterson E. E. (1965, Chemical Reaction Analysis, Prentice_Hall, N.J). Es una forma muy estructurada de presentar los elementos básicos del modelo y su interrelacion en una sola tabla, como se muestra a continuación (Tabla I).

En la tabla se enlistan:

1. Los i componentes: oxígeno disuelto, sustrato soluble y biomasa, con su simbología en la primera línea y su descripción y unidades en la última.


2. Los j procesos en la primera columna: crecimiento bacteriana y decaimiento.


3. En el centro de la matriz se dan los coeficientes estequiométricos ν _ji para cada proceso j, respecto a cada componente i.
   ejemplo: El proceso de crecimiento puede escribirse: ν₁₁ O + ν₁₂ S --> ν₁₃ X


4. Última columna: eX_Presiones de la ley de velocidad de cada proceso, ρ_j.


5. En la misma matriz se consignan también la nomenclatura de los componentes y definición de los parámetros cinéticos.

Cuando las unidades se escogen de forma consistente (por ejemplo en DQO), se puede verificar la continuidad y determinar el valor de los ν_ji incógnitos a partir de la ecuación que iguala a cero la suma de los coeficientes de cada línea (Σν_ji = 0 para DQO). Para cada proceso, uno de los coeficientes puede fijarse a 1 ó -1 mientras que se calculan los demás. Por convención, ν_ji será negativo para los reactivos y positivo para los productos.
El chequeo de continuidad se hace recorriendo las líneas de la matriz: Por ejemplo, para el crecimiento, Σν_ji = 0, &rarr 1 + (-1/Y) + (-1)*(-(1-Y)/Y) = 0. El último cociente se multiplica por (-1) por lo que la “DQO del oxígeno es negativa”, no es demanda, es disponibilidad. La continuidad para el decaimiento muestra que la descripción del proceso, tal como está dada en la tabla, es incompleta (falta representar los productos).

Abajo de cada columna, se puede calcular la tasa neta de conversión de cualquier componente i como resultante de los diferentes procesos j: r_{i neta} = Σν_ji ρj…   Por ejemplo, la tasa neta de utilización de oxígeno (ro₂) debida al consumo ocasionado, tanto por el crecimiento como por la respiración endógena, será dada por la siguiente eX_Presión:

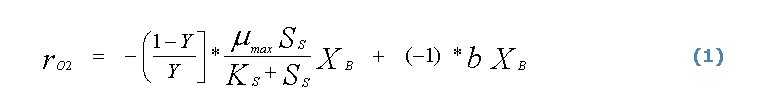
La tasa neta de conversión es sólo la componente del balance de masa respecto a los procesos de transformación; falta añadir los términos de transporte y de acumulación para tener la ecuación completa de balance de masa. Por ejemplo, en el caso de un reactor de mezcla completa sin recirculación, los balances de biomasa activa X_b, y de sustrato S_S vienen dados por el siguiente sistema de ecuaciones diferenciales acopladas:

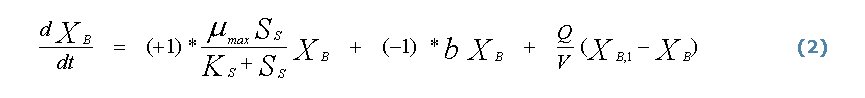
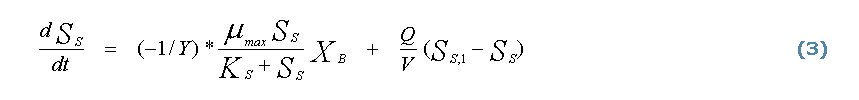
El índice “1” de los parámetros indica los valores en el influente. V es el volumen del reactor y Q el caudal de aguas residuales; t representa el tiempo.

La necesidad de programas para resolver los sistemas de ecuaciones se aprecia con este ejemplo simple, y aún más cuando se escribe la totalidad de los balances para los j compuestos, y que además se utilizan eX_Presiones no simplificadas de las leyes cinéticas.

Funciones de activación y desactivación

Para ilustrar estas nociones se toma como ejemplo la eX_Presión cinética utilizada en el ASM 1 para el proceso de crecimiento en medio anóxico (ecuación 4).

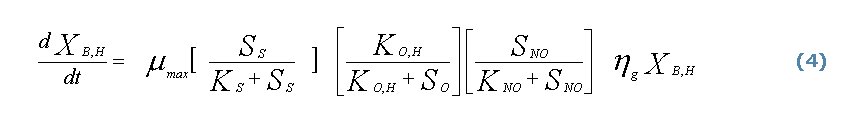
X_B,H: biomasa heterótrofa activa
S_S: sustrato fácilmente biodegradable
S_O: concentración de oxígeno disuelto
S_NO: concentración de nitratos
ηg: factor de corrección de crecimiento en medio anóxico.
t : tiempo
K_S, K_OH, K_NO: constantes de media saturación o de activación/desactivación

El crecimiento conjuntado al mecanismo de desnitrificación en un tanque anóxico ocurre con una velocidad que aumenta con la concentración de sustrato (DQO) y de nitratos presentes en el reactor, mientras que viene perjudicado por cualquier presencia de oxígeno disuelto. Para representar estos efectos se utilizan funciones matemáticas de activación y desactivación como los representados entre los [], siendo los valores de los K, cantidades pequeñas. La primera función K_O,H/(K_O,H + S_O) ocasiona que las altas concentraciones de oxígeno disuelto provoquen una tendencia de la tasa de crecimiento a cero (desactivación), mientras que la presencia nula de O2 permite que la función llegue a su máximo que es 1 (activación). En el caso de la segunda función S_NO/(K_NO+ S_NO) con respecto a los nitratos, ocurre lo contrario; la activación se realiza en altas concentraciones de nitratos mientras que la desactivación está relacionada con la ausencia del mismo compuesto. Estas dos formas de funciones (activación /desactivación vs desactivación/activación) representan los dos tipos que se utilizan en las eX_Presiones cinéticas, para traducir el efecto de varios parámetros. Aun si se parecen a la ecuación de Monod o a su inverso, son utilizadas antes de todo por su conveniencia matemática que por algún tipo de fundamento biológico.

La selección de algún pequeño valor más que otro para las constantes K suele realizarse con base en la búsqueda de lograr predecir de forma correcta la producción de lodo y la demanda de oxígeno (se hayan por calibración en escala real por opuesto a varios parámetros cinéticos que se determinan con los estudios de laboratorio).

Existen varias versiones modificadas del modelo ASM1 donde los autores extienden la utilización de las funciones de activación para tomar en cuenta algún otro parámetro que haya demostrado un efecto significativo en su caso especifico (pH, Alcalinidad, etc.).

La DQO fraccionada como parámetro de caracterización

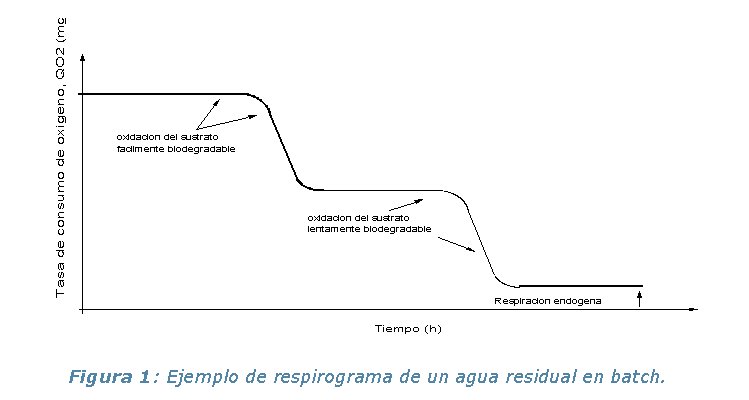
Uno de los desarrollos más significativos, logrado para mejorar la comprensión del proceso de lodos activados fue la adopción de la DQO como componente modelo para el sustrato. Entre la DBO, COT y DQO, el task group propuso utilizar la demanda química de oxígeno, porque primero es el único que permite establecer una liga clara entre los equivalentes de electrones entre el sustrato orgánico, la biomasa activa y el oxígeno utilizado (Task group 1987, Ubay Cokgor et al. 1998). De esta forma se pueden realizar balances de masas que cierren. La prueba de DQO es además rápida y repetible. Sin embargo, se había ya observado claramente que la DQO total, sola como tal, no es suficiente para predecir bien la producción de lodo y el consumo de oxígeno. Se sabía que la materia orgánica es muy heterogénea, siendo formada por una larga gama de compuestos, pero las observaciones eX_Perimentales permitieron llegar al consenso de que la materia orgánica biodegradable puede representarse dividiéndola en solo dos grupos de compuestos (modelo bi-sustrato) que tienen una diferencia muy marcada entre sus tasas de degradación (Ubay Cokgor et al. 1998). Los dos grupos fueron identificados como la fracción de DQO fácilmente biodegradable y su contraparte lentamente biodegradable. Las evidencias respirométricas que fueron a la base de esta decisión se ilustran con la figura 1 donde se pueden observar dos mesetas para el nivel de QO2, cada una representando la degradación de uno de los dos grupos antes mencionados.

Modelo ASM n°1 del proceso de lodos activados
Presentación general del modelo

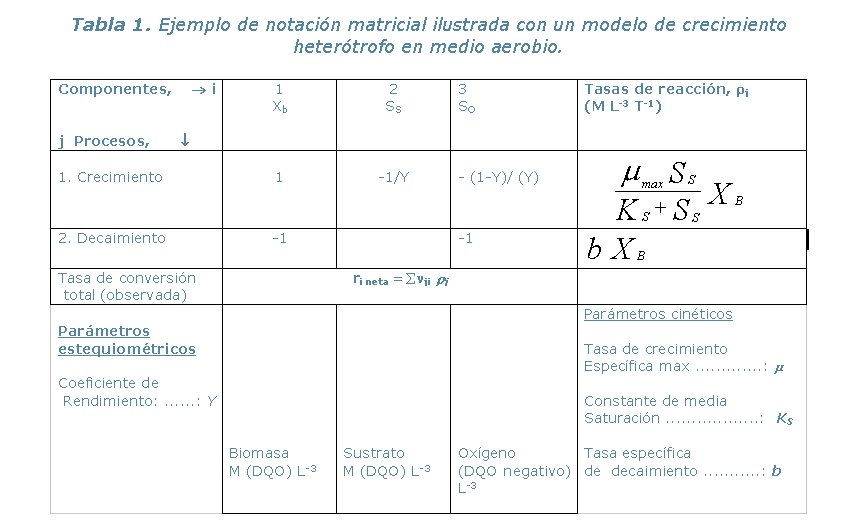
El modelo ASM1 fue desarrollado por el Task group en 1987. Tiene como propósito simular la degradación de la materia orgánica así como la nitrificación y desnitrificación de los procesos de lodos activados de tipo lodos únicos. El modelo fue presentado utilizando la notación matricial (Tabla II). El modelo cuenta con:

• 13 componentes en total: 7 disueltos y 6 de partículas


• 9 procesos: 3 de crecimiento, 2 de decaimiento y 4 de hidrólisis.

Los componentes del modelo N°1

Son 13 componentes que incluyen 7 disueltos y 6 con una forma de partículas. Dentro de los 13 componentes los 7 primeros se relacionan con las sustancias carbonosas del agua y del lodo (medidos en DQO) mientras que existen 4 constituyentes nitrogenados además del oxígeno y de la alcalinidad. El parámetro de alcalinidad no es esencial al modelo, es sólo una información adicional añadida para permitir detectar indirectamente los riesgos de cambio en el pH.

El material carbonoso del modelo está dividido en un primer tiempo en DQO biodegradable, DQO no biodegradable (materia orgánica inerte) y Biomasa (Figura 2).

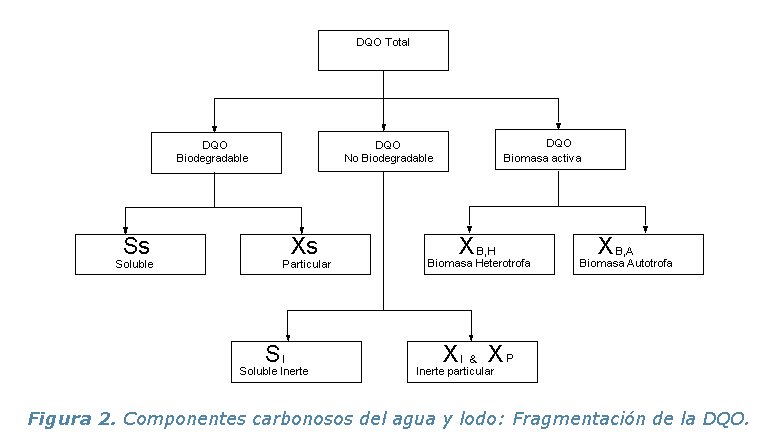
La parte biodegradable está luego dividida en una fracción rápidamente biodegradable (Ss soluble) y en una fracción lentamente biodegradable (X_s, particulada). Se toma como hipótesis que la fracción rápidamente biodegradable está compuesto de materia orgánica soluble que se adsorbe y metaboliza rápidamente por los microorganismos mientras que la fracción X_s compuesta de partículas, coloides y materia orgánica compleja, sufre una hidrólisis enzimática antes de poder ser adsorbida. En realidad, la fracción lentamente biodegradable incluye compuestos orgánicos solubles difícilmente biodegradables que se tratan como si fueran materia particulada.

La fracción no biodegradable de la DQO está dividida en una fracción soluble inerte (S_I) y en una fracción particulada (X_I). Los dos no son afectados por el proceso. SI abandona la planta con el efluente del sedimentador secundario mientras que X_I se enreda en el lodo purgado y contribuye a los sólidos volátiles (SSV).

La biomasa activa se divide en dos tipos de grupos de microorganismos: heterótrofos (X_B,H) y autótrofos (X_B,A). Por ende, una variable adicional, X_P, está introducida para modelizar la fracción inerte de productos procedentes del decaimiento de la biomasa. En la realidad, no se puede diferenciar X_P de X_I en el lodo.

La fragmentación del material nitrogenado se representa en la Figura 3.

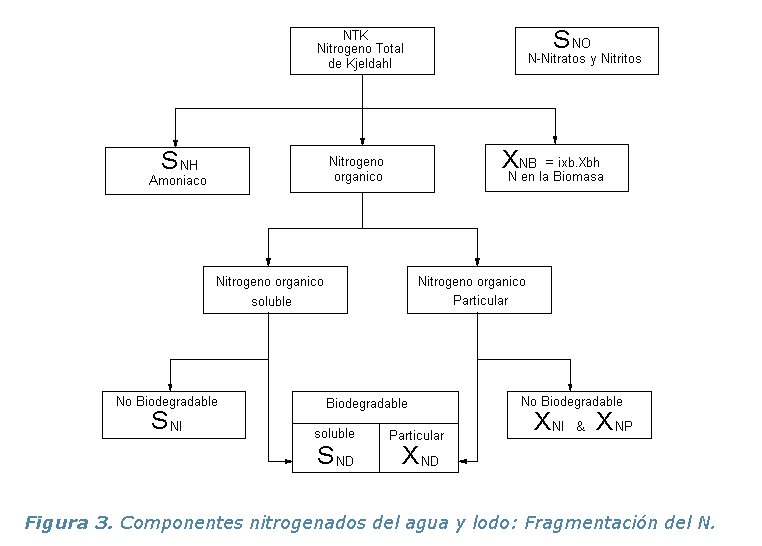
El nitrógeno total presente en el sistema incluye por un lado los nitratos y nitritos (S_NO) y por otro el nitrógeno total de Kjeldahl (NTK). Los nitratos y nitritos se combinaron en un solo componente para simplificar el modelo. Algunos autores utilizan versiones modificadas del modelo con una separación entre estos dos productos.

El nitrógeno total de Kjeldahl se fragmenta en nitrógeno amoniacal (S_NH, que incluye el N-NH₄+ y N-NH₃), nitrógeno orgánico y nitrógeno contenido en la biomasa. De forma idéntica a la materia orgánica carbonosa (DQO), el nitrógeno orgánico se divide en una fracción soluble y otra particulada, cada uno teniendo su fracción biodegradable y no biodegradable. Son únicamente las fracciones biodegradables, soluble (S_ND) y particulada (X_ND), que aparecen de forma eX_Plícita en el modelo. El nitrógeno de la biomasa activa (X_NB) se toma en cuenta de forma indirecta en el sentido que el decaimiento produce nitrógeno orgánico particulada biodegradable (1-fp). El nitrógeno orgánico asociado a la fracción de productos inertes particuladas (X_NP), así como el N asociado a la fracción inerte de materia orgánica (X_NI) se pueden calcular fácilmente, aun si no se muestran en la matriz del modelo.

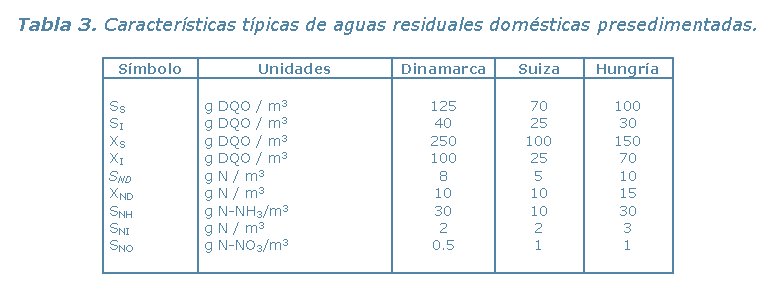
En la Tabla 3 se muestran algunas características típicas de aguas residuales domésticas primarias (presedimentadas).

Los procesos del modelo No.1

El ASM1 original incluye 8 procesos que se pueden reagrupar en cuatro tipos:

1. 1. Procesos de crecimiento (tres).


2. Procesos de decaimiento (dos).


3. Procesos de hidrólisis de partículas enredadas en los bio-flocs (dos).


4. Proceso de amonificación (uno).

Los diferentes procesos se describen a continuación:

• Crecimiento aerobio de los heterótrofos.
  Se considera que sólo S_S interviene en el crecimiento de los heterótrofos. X_S debe sufrir una hidrólisis (tardada) antes de que pueda transformarse en SS y ser utilizado por los microorganismos. El crecimiento se modeliza utilizando la estructura del modelo de Monod donde pueden ser limitantes tanto S_S, como S_O (el oxígeno). Este proceso es el que más contribuye en la remoción de DQO, producción de biomasa nueva y demanda de oxígeno. El nitrógeno amoniacal se consume en el proceso de crecimiento por su incorporación en las células mientras que cambia también la alcalinidad.



• Crecimiento anóxico de los heterótrofos.
  En la ausencia de oxígeno, los organismos heterótrofos son capaces de utilizar los nitratos como aceptor terminal de electrones con S_scomo sustrato. El proceso resulta en una producción suplementaria de biomasa heterótrofa y de nitrógeno gaseoso (desnitrificación). El último resulta de la reducción de los nitratos con su cambio subsecuente en la alcalinidad. Se utilizan las mismas eX_Presiones cinéticas de tipo Monod respecto al sustrato asociado a funciones de activación/desactivación respecto a los nitratos y oxígeno. Se utiliza un factor de corrección η_g (<1)para tomar cuenta del hecho que la tasa máxima de crecimiento de los heterótrofos es menor en medio anóxico. El amoniaco y la alcalinidad sufren también cambios por las mismas razones que las anteriores.



• Crecimiento aerobio de los autótrofos.
  El amoniaco se oxida en nitratos vía un proceso de nitrificación a etapa única, resultando en la producción de biomasa autótrofa nueva y un consumo adicional de oxígeno. El amoniaco se incorpora también en las células. El proceso tiene un efecto marcado en el balance de alcalinidad y en el consumo de O₂ mientras que la contribución en la formación de lodo es pequeña debido que la tasa de crecimiento de los autótrofos es muy baja. El modelo es de tipo Monod respecto al amoniaco y oxígeno (caso que es también una función de activación).



• Decaimiento de los heterótrofos.
  La noción de decaimiento en este modelo incluye todos los fenómenos de lísis, respiración endógena, muerte o depredación. Su tratamiento matemático en el ASM1 es diferente del enfoque tradicional donde se le atribuía directamente un consumo de O₂ (respiración endógena). La modelación en el ASM1 utiliza la noción de muerte-regeneración, donde X_B &rarr X_S + X_P sin consumo directo de O₂. El consumo de O₂ está diferido hasta después que el Xs se transforma en Ss (hidrólisis) y que Ss se utiliza en el proceso de crecimiento. Por eso, el valor de bH del modelo tiene mucha diferencia con respecto al valor empleado en los modelos tradicionales (b´H). El proceso manifiesta ninguna pérdida de DQO, ni consumo directo de O₂; por el contrario, produce residuos orgánicos inertes (X_P) y una DQO lentamente biodegradable (X_s). Se supone que el proceso ocurre con la misma velocidad en condiciones aerobias que anóxicas. El modelo utilizado es de orden 1 respecto a la biomasa.



• Decaimiento de los autotrófos.
  El proceso se modeliza de la misma forma que para los heterótrofos.



• Amonificación del nitrógeno orgánico soluble, S_ND.
  Se modeliza con una cinética de orden 1 respecto a S_ND y respecto a la biomasa heterótrofa. Es frecuente que se omita este proceso en las versiones modificadas del ASM1 debido a su rapidez.



• Hidrólisis de la materia orgánica.
  La materia orgánica particulada lentamente biodegradable (X_s) se encuentra enredada en los flocs biológicos donde sufre un rompimiento y solubilización por efecto de las enzimas extracelulares. El resultado es la producción de sustrato soluble fácilmente biodegradable que se utiliza luego en el crecimiento. La estructura del modelo utilizado para este proceso es típica de los procesos de superficie (adsorción). Es también de orden 1 respecto a la biomasa pero tiende a saturarse cuando la cantidad de sólidos enredados en los flocs (X_s) viene a ser grande comparado a la biomasa (X_BH). La hidrólisis es un proceso que ocurre tanto en condiciones aerobias como en condiciones anóxicas. Se utiliza un factor de corrección η_h (<1) para tomar en cuenta el hecho de que la tasa de hidrólisis es menor en medio anóxico comparado al medio aerobio.



• Hidrólisis del nitrógeno orgánico particulado.
  El nitrógeno orgánico particulado (X_ND) es parte de la materia orgánica particulada (X_S), por lo que la tasa de hidrólisis del primero está determinada por la tasa de hidrólisis (ρ₇) del segundo componente. El modelo utilizado muestra una proporcionalidad entre las dos tasas.

Origen y cambios sufridos por los componentes

En este apartado, se hacen comentarios respecto al origen y futuro de los componentes refiriéndose por eso a las columnas de la matriz del modelo.

Componentes orgánicos del agua

La materia orgánica en el agua residual está compuesta de:

Columna 1 y 3. S_I y X_I no participan en ninguna conversión, pero S_I contribuye a la calidad del efluente y X_I es parte de los sólidos volátiles del licor mixto y de los lodos purgados.

Columna 2. SS se utiliza en el crecimiento de la biomasa heterótrofa en condiciones aerobias y en condiciones anóxicas. Además de la cantidad inicial presente en el influente, S_S se genera continuamente como producto de la hidrólisis de la materia orgánica particulada X_S.

Columna 4. X_S se consume por hidrólisis pero se forma como producto de la lísis de la biomasa heterótrofa y autótrofa.

Componentes orgánicos de biomasa

La biomasa activa presente en el agua residual y en el licor mixto se caracteriza con los siguientes componentes:

Comúnmente se suele despreciar el aporte de biomasa activa por el influente. Por otro lado, la DQO total y los sólidos suspendidos volátiles (SSV) del lodo purgado y licor mixta están formados por la biomasa activa y biomasa inactiva: X_B,H + X_B,A + X_P + X_I + X_S.

Columna 5 y 6. La biomasa heterótrofa XB,H y autótrofa X_B,A, se forman a partir del crecimiento aerobio, por un lado, y anóxico (sólo por X_B,H) por otro, mientras que se pierden por el proceso de decaimiento.

Columna 7. Al decaer, X_B,H y X_B,A dejan formarse entre otros productos, un residuo particulado inerte X_P que no participa en ninguna otra conversión (contribuye a la biomasa inactiva).

Oxígeno disuelto

Columna 8. El oxígeno está consumido en el crecimiento de los heterótrofos y autótrofos. El modelo no considera que se consume oxígeno directamente en el decaimiento (sólo indirectamente a través de Ss que proviene de la lísis). El modelo, como se ha representado, permite determinar el consumo de oxígeno (rO₂), pero no las variaciones en la concentración de oxígeno, So. Para poder predecir So, se necesita incluir el proceso de aireación en el modelo.

Los compuestos nitrogenados.

Para el agua dentro del sistema de tratamiento, el modelo considera las siguientes cuatro formas de nitrógeno biodegradables:

Fuera de estas formas que se contemplan en la matriz, existen otras tres formas de nitrógeno orgánico que son las incorporadas en la biomasa (X_NB = iXB .XB), en los productos inertes de lisis (X_NP = X_P .iX_P) y en la fracción de materia orgánica inerte (XNI = XI .iXI). Estas formas fácilmente calculables no son necesarias en el modelo puesto que no se puede hacer un chequeo del balance de nitrógeno, a menos que se capte y cuantifique el nitrógeno gaseoso del proceso (N2).

Columna 9 (S_NO). El segundo recibidor de electrón que incluye al modelo está formado de los nitratos (y nitratos). Están producidos en el crecimiento aerobio de los autótrofos y removidos en el crecimiento anóxico de los heterótrofos. El factor 2.86 que aparece en uno de los coeficientes estequiométricos corresponde al equivalente en O2 de la conversión de NO3 en N2.

Columna 10. El nitrógeno amoniacal (S_NH) utilizado proviene de la reacción de amonificación del nitrógeno orgánico soluble y se consume principalmente cuando sirve de fuente de energía en el crecimiento de la biomasa autótrofa. Hay que contar también una fracción (iXB) de NH₄+ que se incorpora en las células durante la síntesis. Se considera que a pH ˜ 7.0, S_NH es formado principalmente del ion amonium NH₄+. Como simplificación, el modelo número 1 considera que la formación de NO₃ se hace directamente sin otra etapa que pasa por el N₂.

Columna 11. El nitrógeno orgánico soluble (S_ND) es producto de la hidrólisis de su forma particulada (X_ND) mientras que es removido por la amonificación.

Columna 12. X_ND se pierde de la solución por hidrólisis, pero se reacumula con la muerte de los microorganismos, tanto autótrofos como heterótrofos, donde se recupera el equivalente de i_XB - .fP •i_XP. El producto fP•i_XP es la fracción que no está recuperable, porque está asociada a la fracción inerte de los productos de lísis.

4.4.5 Alcalinidad

Columna 13. Representa el balance de alcalinidad (S_alk), por lo que sería complicado incluir en el modelo, partes que permitan prever directamente las variaciones de pH. Se optó por hacer el balance de alcalinidad, pudiendo obtener de éste, señales sobre el pH. Para fines prácticos, se considera que una caída de 50 mg/L de CaCO₃ en la alcalinidad puede causar inestabilidad y caída del pH a valores menores que 6, lo que podría afectar de forma significativa el proceso de nitrificación.

Utilización del modelo ASM1

Antes de poder utilizar el modelo para simular una planta de tratamiento en particular, se debe realizar la calibración del mismo, actividad que lleva varios pasos. No se podría abordar de forma sistemática y completa este tema amplio en el contexto de este curso. A continuación se dan algunas indicaciones sobre los procedimientos a llevar a cabo, así como algunas referencias importantes para quien quiere profundizar sobre el tema.

Caracterización de las aguas y determinación de los parámetros del modelo

Uno de los pasos más importantes en los proyectos de modelación de plantas de tratamiento de aguas es la calibración, la cual puede llevar largas horas de muestreo, análisis y eX_Perimentos en el laboratorio y en planta para determinar varios de los parámetros cinéticos, estequiométricos y caracterizar las aguas. Un procedimiento eX_Perimental para determinar cada uno de los parámetros, está descrito en el informe del Task group (Task group 1987). La determinación de los parámetros cinéticos en general, y la caracterización del agua, en particular (según el principio de fragmentación de la DQO), se llevan a cabo utilizando eX_Perimentos de respirometría.

La utilidad y exactitud de los modelos se juzga principalmente por su habilidad a bien predecir la producción de lodos y sobre todo la demanda de aceptor de electrones (oxígeno y nitratos). Por lo tanto, la técnica de respirometría juega un papel fundamental en casi la mayoría de las determinaciones de parámetros y características de las aguas y lodos (Spanjers et al. 1998).

Varias de las técnicas eX_Puestas en el documento original del modelo ASM1 son complejas pero no eran propuestas definitivas. En la literatura más reciente, se puede encontrar algunos métodos alternativos para varios de los parámetros del modelo (Ubay-Cokgor et al. 1999, Sollfrank y Gujer 1991, Vanrolleghem et al. 1999, Kappeler y Gujer 1992, Sperandio et al 2001, entre otros). En los procedimientos alternativos más recientes, suele ser frecuente la utilización de la repirometría para determinar los parámetros.

Al inicio, la utilización de los procedimientos presentados en el documento del Task Group ha permitido hallar y proponer una lista de parámetros de “default” que uno puede utilizar para fines de simulación general o inicio de estudios de calibración. Estos datos se presentan en la tabla 4.

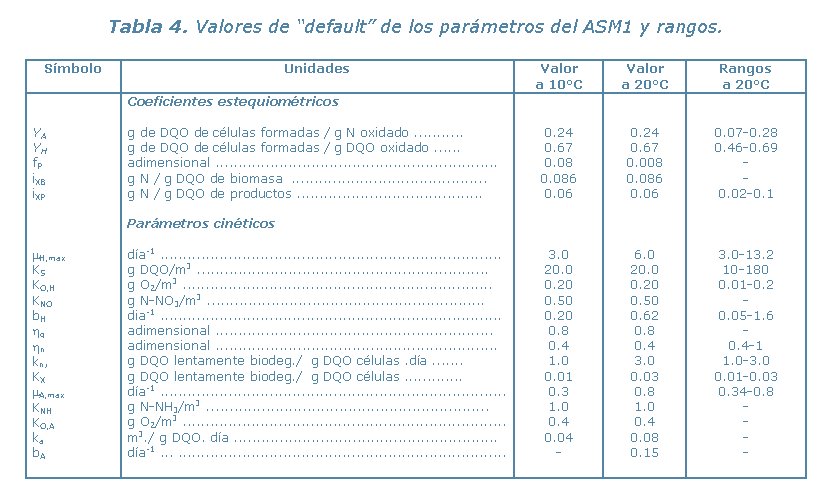
Dentro de la lista de parámetros, el Task Group identificó un cierto número de ellos, cuyo valor, no muy variable de una agua a otra, puede suponerse igual al valor de “default”, necesitando sólo hallar el valor de los demás parámetros, para el caso específico de planta de tratamiento que se está calibrando. Los parámetros que se pueden tomar como supuestamente fijos son: Y_A, f_P, i_XB, i_XP, K_O,H, K_NO, K_O,A, b_A

Los datos de la tabla se consideran típicos para un pH cercano de la neutralidad y para aguas municipales. El Task Group reconoce que existe un cierto riesgo en la utilización generalizada de estos valores debido a que son fuertemente influenciados por las condiciones específicas del agua residual, en particular la temperatura, el pH y los compuestos presentes en el agua. Estos valores pueden utilizarse sólo cuando no existen datos específicas. No se ha demostrado la aplicabilidad del modelo para las aguas residuales industriales y menos para los valores de “default”.

Protocolo de simulación de plantas de tratamiento

La implementación del modelo para simular plantas de tratamiento debe de realizarse siguiendo una metodología ordenada. Un ejemplo de protocolo que se podría seguir, uno de los pocos publicados, es el propuesto por la STOWA (Fundación holandesa de investigación aplicada en agua) y utilizado en Holanda para simular las plantas de tratamiento de aguas municipales a gran escala (Hulsbeek et al 2002). La figura 4 representa los pasos, los cuales que se detallan en el documento referido.

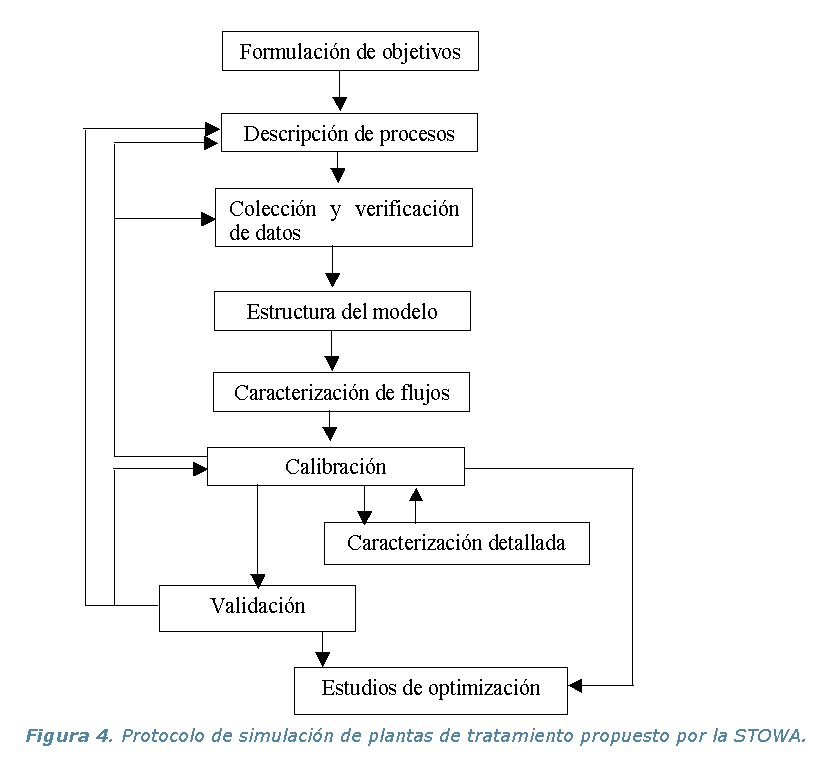
Varias de las plantas de tratamiento de aguas municipales de Holanda han sido modelizadas, permitiendo acumular una eX_Periencia sin precedente en el tema (más de 100 plantas en los últimos cinco años), lo que permitió a la STOWA elaborar un protocolo consensual fácil de usar.

El protocolo es útil para servir de guía en todo lo relacionado con el procedimiento general de modelación, pero también lleva varias particularidades que lo desapegan de los procedimientos de calibración y caracterización del documento del ASM1:

1° Después de constatar que la simulación en planta real no es sensible a una evaluación exacta de la partición entre Xs y Ss, propusieron una metodología de caracterización mucho más simple, en la cual se utilizan análisis físico-químicos y mediciones de la curva de DBO, al lugar de la respirometría (Roeleveld et al 2002). Se reconoce que los datos hallados de esta forma podrían no ser aplicables a eX_Perimentos a pequeña escala como los estudios de laboratorio.

2° Notaron que la simulación en planta es mucho más sensible a los datos de caudales, los cuales deben ser verificados y confirmados con balances de masas (Meijer et al 2002). La simulación es poco sensible a varios de los parámetros cinéticos o características del agua. Los autores sugieran calibrar el modelo directamente en la planta, empezando con los valores de “default” y ajustando algunos parámetros específicos:

a) Medir y calibrar la composición y cantidad de lodo, ajustando X_s y X_i del influente, así como i_XB y i_XI.
b) Medir y calibrar el amoniaco del efluente, ajustando K_O,H, K_NH y bA.
c) Medir y calibrar la concentración de nitratos en el efluente, ajustando ηg, bH, K_O,A, K_O,H.

En el caso de que los parámetros necesiten ser ajustados fuera de los rangos típicos, se considera que en el caso de Holanda es muy probable que el problema se ubicque en los datos de caudales.

Bibliografía

Task Group (1987). Henze M., Gujer W., Mino T. and Van Loosdrecht M.V. (2002). Activated sludge models ASM1, ASM2, ASM2d and ASM3. IAWQ scientific and tecnical report N° 9, edited by IWA Task Group on mathematical modelling for design and operation of biological wastewater treatment, IWA publishing, London, UK, 130 p.
Task Group (2002). Anaerobic Digestion model N°1, IAWQ scientific and tecnical report N° 13, edited by IWA Task Group on mathematical modelling of anaerobic disgestion processes, IWA publishing, London, UK, 80 p.
Meijer S.C.F., Van Loosdrecht M.C.M. and Heijnen J.J. (2001). Metabolic modelling of full-scale biological nitrogen and phosphorus removing WWTP´s. Wat. Res. Vol. 35 (11), pp 2711-2723.
Reichert P., Borchardt D., Henze M., Rauch W., Shanahan P., Somlyódy L. and Vanrolleghem P.A. (2001). River Water Quality Model N° 1, IAWQ scientific and tecnical report N° 12, edited by IWA Task Group on River Water Quality Modelling, IWA publishing, London, UK, 136 p.
Reichert P., Von Schulthess R. and Wild D. (1995). The use of AQUASIM for estimating parameter of activated sludge models, Wat. Sci. Tech. Vol. 31 (2), pp 135-137.
Reichert P., (1998). AQUASIM 2.0 -Tutorial, computer program for the identification and simulation of aquatic systems, Swiss Federal Institutute for Environmental Science and Technology (EAWAG), Switzerland.
Roeleveld P.J. and Van Loosdrecht M.C.M. (2002). EX_Perience with guidelines for wastewater characterization in the Netherlands. Wat. Sci. Tech. Vol. 45 (6), pp 77-87.
Hulsbeek J.J.W., Roeleveld P.J. and Van Loosdrecht M.C.M. (2002). A practical protocol for dynamic modelling of activated sludge systems. Wat. Sci. Tech. Vol. 45 (6), pp 127-136.
Sollfrank U. and Gujer W. (1991). Characterization of domestic wastewater for mathematical modelling of the activated sludge process, Wat. Sci. Tech. Vol. 23, pp 1057-1066.
Spanjers H., Vanrolleghem P.A., Olsson G. and Dold P.L. (1998). Respirometry in control of the activated sludge process: principles. IAWQ scientific and tecnical report N° 7, IAWQ Task Group on Respirometry, IAWQ, London, UK, 48 p.
Van Loosdrecht M.C.M y Henze M. (1999). Maintenance, endogeneous respiration, lysis, decay and predation. Wat. Sci. Tech. Vol. 39 (1), pp 107-117.
Petersen, E.E. (1965). Chemical Reaction Analysis. Prentice-Hall, Englewood Cliffs, NJ, USA.
Ubay-Cokgor E., Sozen S., Orhon D. and Henze M. (1998). Respirometric Analisis of activated sludge behaviour. I. Assessment of the readily biodegradqable substrate, Wat. Res. Vol. 32 (2), pp 461-475.